Simple Random Sampling | Definition, Steps & Examples
A simple random sample is a randomly selected subset of a population. In this sampling method, each member of the population has an exactly equal chance of being selected, minimising the risk of selection bias.
This method is the most straightforward of all the probability sampling methods, since it only involves a single random selection and requires little advance knowledge about the population. Because it uses randomisation, any research performed on this sample should have high internal and external validity.
When to use simple random sampling
Simple random sampling is used to make statistical inferences about a population. It helps ensure high internal validity: randomisation is the best method to reduce the impact of potential confounding variables.
In addition, with a large enough sample size, a simple random sample has high external validity: it represents the characteristics of the larger population.
However, simple random sampling can be challenging to implement in practice. To use this method, there are some prerequisites:
- You have a complete list of every member of the population.
- You can contact or access each member of the population if they are selected.
- You have the time and resources to collect data from the necessary sample size.
Simple random sampling works best if you have a lot of time and resources to conduct your study, or if you are studying a limited population that can easily be sampled.
In some cases, it might be more appropriate to use a different type of probability sampling:
- Systematic sampling involves choosing your sample based on a regular interval, rather than a fully random selection. It can also be used when you don’t have a complete list of the population.
- Stratified sampling is appropriate when you want to ensure that specific characteristics are proportionally represented in the sample. You split your population into strata (for example, divided by gender or race), and then randomly select from each of these subgroups.
- Cluster sampling is appropriate when you are unable to sample from the entire population. You divide the sample into clusters that approximately reflect the whole population, and then choose your sample from a random selection of these clusters.
How to perform simple random sampling
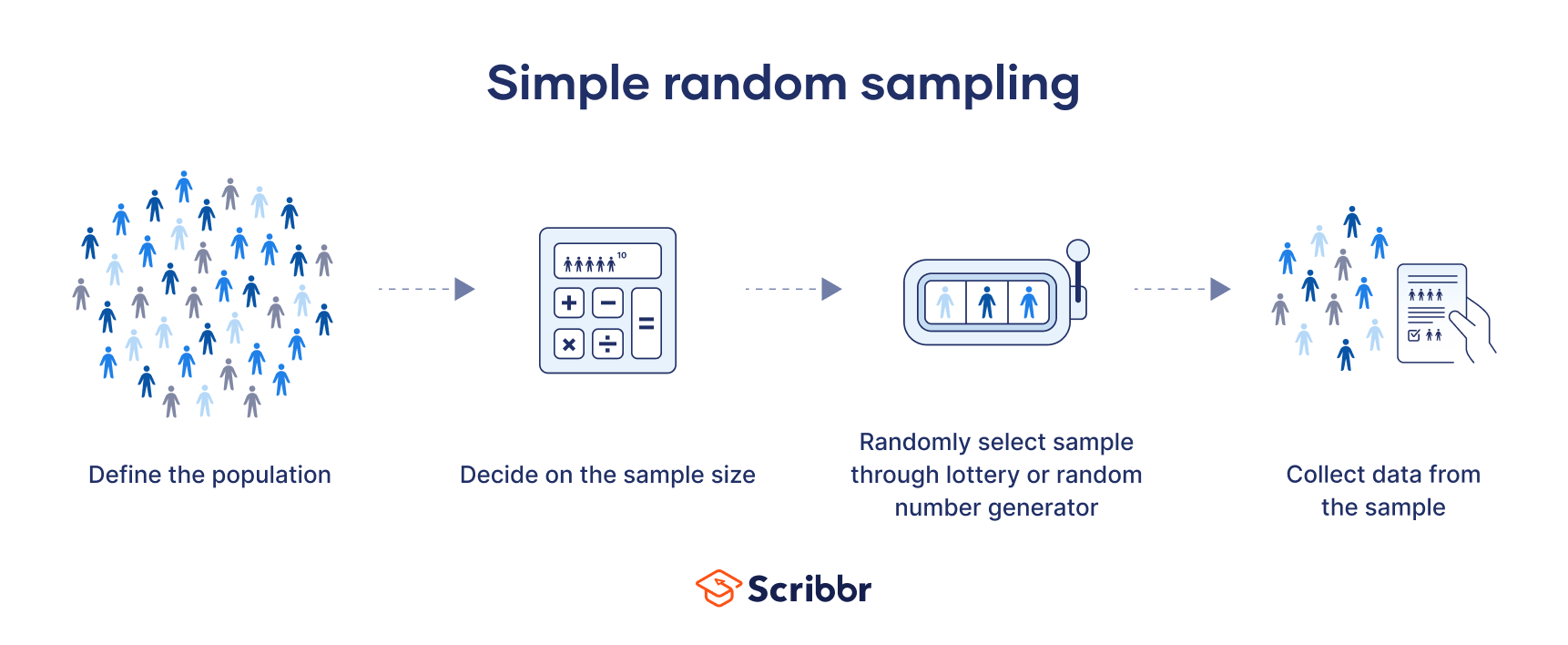
There are four key steps to select a simple random sample.
Step 1: Define the population
Start by deciding on the population that you want to study.
It’s important to ensure that you have access to every individual member of the population, so that you can collect data from all those who are selected for the sample.
Step 2: Decide on the sample size
Next, you need to decide how large your sample size will be. Although larger samples provide more statistical certainty, they also cost more and require far more work.
There are several potential ways to decide upon the size of your sample, but one of the simplest involves using a formula with your desired confidence interval and confidence level, estimated size of the population you are working with, and the standard deviation of whatever you want to measure in your population.
The most common confidence interval and levels used are 0.05 and 0.95, respectively. Since you may not know the standard deviation of the population you are studying, you should choose a number high enough to account for a variety of possibilities (such as 0.5).
You can then use a sample size calculator to estimate the necessary sample size.
Step 3: Randomly select your sample
This can be done in one of two ways: the lottery or random number method.
In the lottery method, you choose the sample at random by ‘drawing from a hat’ or by using a computer program that will simulate the same action.
In the random number method, you assign every individual a number. By using a random number generator or random number tables, you then randomly pick a subset of the population. You can also use the random number function (RAND) in Microsoft Excel to generate random numbers.
Step 4: Collect data from your sample
Finally, you should collect data from your sample.
To ensure the validity of your findings, you need to make sure every individual selected actually participates in your study. If some drop out or do not participate for reasons associated with the question that you’re studying, this could bias your findings.
For example, if young participants are systematically less likely to participate in your study, your findings might not be valid due to the underrepresentation of this group.
Through this variety of methods, the officials collecting data for the ACS manage to receive responses from 95% of those randomly selected, a high response rate that supports the validity of their results.
Frequently asked questions about simple random sampling
- What is probability sampling?
-
Probability sampling means that every member of the target population has a known chance of being included in the sample.
Probability sampling methods include simple random sampling, systematic sampling, stratified sampling, and cluster sampling.
- What is simple random sampling?
-
Simple random sampling is a type of probability sampling in which the researcher randomly selects a subset of participants from a population. Each member of the population has an equal chance of being selected. Data are then collected from as large a percentage as possible of this random subset.
- What is an example of simple random sampling?
-
The American Community Survey is an example of simple random sampling. In order to collect detailed data on the population of the US, the Census Bureau officials randomly select 3.5 million households per year and use a variety of methods to convince them to fill out the survey.
- When should I use simple random sampling?
-
If properly implemented, simple random sampling is usually the best sampling method for ensuring both internal and external validity. However, it can sometimes be impractical and expensive to implement, depending on the size of the population to be studied,
If you have a list of every member of the population and the ability to reach whichever members are selected, you can use simple random sampling.
- Why are samples used in research?
-
Samples are used to make inferences about populations. Samples are easier to collect data from because they are practical, cost-effective, convenient, and manageable.
- What is sampling bias?
-
Sampling bias occurs when some members of a population are systematically more likely to be selected in a sample than others.
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Thomas, L. (2023, December 18). Simple Random Sampling | Definition, Steps & Examples. Scribbr. Retrieved 9 December 2024, from https://www.scribbr.co.uk/research-methods/simple-random-sampling-method/