Stratified Sampling | A Step-by-Step Guide with Examples
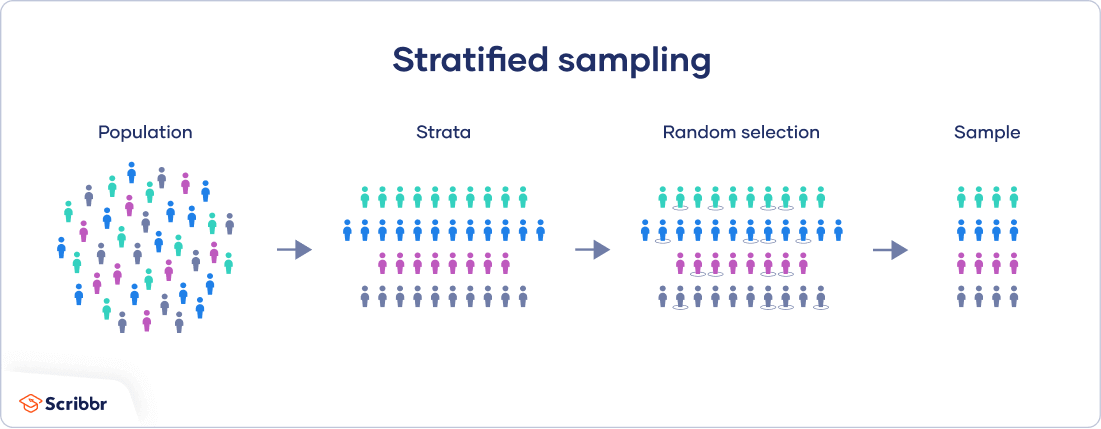
In a stratified sample, researchers divide a population into homogeneous subpopulations called strata (the plural of stratum) based on specific characteristics (e.g., race, gender identity, location). Every member of the population studied should be in exactly one stratum.
Each stratum is then sampled using another probability sampling method, such as cluster or simple random sampling, allowing researchers to estimate statistical measures for each subpopulation.
Researchers rely on stratified sampling when a population’s characteristics are diverse and they want to ensure that every characteristic is properly represented in the sample.
When to use stratified sampling
To use stratified sampling, you need to be able to divide your population into mutually exclusive and exhaustive subgroups. That means every member of the population can be clearly classified into exactly one subgroup.
Stratified sampling is the best choice among the probability sampling methods when you believe that subgroups will have different mean values for the variable(s) you’re studying. It has several potential advantages:
-
Ensuring the diversity of your sample
A stratified sample includes subjects from every subgroup, ensuring that it reflects the diversity of your population. It is theoretically possible (albeit unlikely) that this would not happen when using other sampling methods such as simple random sampling.
-
Ensuring similar variance
If you want the data collected from each subgroup to have a similar level of variance, you need a similar sample size for each subgroup.
With other methods of sampling, you might end up with a low sample size for certain subgroups because they’re less common in the overall population.
-
Lowering the overall variance in the population
Although your overall population can be quite heterogeneous, it may be more homogenous within certain subgroups.
For example, if you are studying how a new schooling program affects the test scores of children, both their original scores and any change in scores will most likely be highly correlated with family income. The scores are likely to be grouped by family income category.
In this case, stratified sampling allows for more precise measures of the variables you wish to study, with lower variance within each subgroup and therefore for the population as a whole.
-
Allowing for a variety of data collection methods
Sometimes you may need to use different methods to collect data from different subgroups.
For example, in order to lower the cost and difficulty of your study, you may want to sample urban subjects by going door to door, but rural subjects by post.
Because only a small proportion of this university’s graduates have obtained a doctoral degree, using a simple random sample would likely give you a sample size too small to properly compare the differences between men, women, and those who do not identify as men or women with a doctoral degree vs those without one.
Therefore, you decide to use a stratified sample, relying on a list provided by the university of all its graduates within the last 10 years.
Step 1: Define your population and subgroups
As with other methods of probability sampling, you should begin by clearly defining the population from which your sample will be taken.
Choosing characteristics for stratification
You must also choose the characteristic that you will use to divide your groups. This choice is very important: since each member of the population can only be placed in only one subgroup, the classification of each subject to each subgroup should be clear and obvious.
Stratifying by multiple characteristics
You can choose to stratify by multiple different characteristics at once, so long as you can clearly match every subject to exactly one subgroup. In this case, to get the total number of subgroups, you multiply the numbers of strata for each characteristic.
For instance, if you were stratifying by both race and gender identity, using four groups for the former and three for the latter, you would have 4 × 3 = 12 groups in total.
Step 2: Separate the population into strata
Next, collect a list of every member of the population, and assign each member to a stratum.
You must ensure that each stratum is mutually exclusive (there is no overlap between them), but that together, they contain the entire population.
Combining these characteristics, you have nine groups in total. Each graduate must be assigned to exactly one group.
| Characteristic | Strata | Groups |
|---|---|---|
| Gender identity |
|
|
| Degree |
|
Step 3: Decide on the sample size for each stratum
First, you need to decide whether you want your sample to be proportionate or disproportionate.
Proportionate vs disproportionate sampling
In proportionate sampling, the sample size of each stratum is equal to the subgroup’s proportion in the population as a whole.
Subgroups that are less represented in the greater population (for example, rural populations, which make up a lower portion of the population in most countries) will also be less represented in the sample.
In disproportionate sampling, the sample sizes of each strata are disproportionate to their representation in the population as a whole.
You might choose this method if you wish to study a particularly underrepresented subgroup whose sample size would otherwise be too low to allow you to draw any statistical conclusions.
Sample size
Next, you can decide on your total sample size. This should be large enough to ensure you can draw statistical conclusions about each subgroup.
If you know your desired margin of error and confidence level as well as estimated size and standard deviation of the population you are working with, you can use a sample size calculator to estimate the necessary numbers.
Even though doctoral students make up a small proportion of the overall student population, your sample is about ⅓ bachelor’s graduates, ⅓ master’s graduates, and ⅓ doctoral graduates.
Step 4: Randomly sample from each stratum
Finally, you should use another probability sampling method, such as simple random or systematic sampling, to sample from within each stratum.
If properly done, the randomisation inherent in such methods will allow you to obtain a sample that is representative of that particular subgroup.
You can then collect data on salaries and job histories from each of the members of your sample to investigate your question.
Frequently asked questions about stratified sampling
Cite this Scribbr article
If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.
Thomas, L. (2022, May 03). Stratified Sampling | A Step-by-Step Guide with Examples. Scribbr. Retrieved 23 June 2025, from https://www.scribbr.co.uk/research-methods/stratified-sampling-method/